컴퓨터그래픽스 2장 - 수학 -

고려대학교 한정현 교수님의 컴퓨터그래픽스 강의 영상을 보고 작성한 포스트입니다 

https://www.youtube.com/watch?v=Jvz0XPSRbx4&list=PLYEC1V9tJOl03WLDoUEKbiYW_Xt4W6LTl&index=1

 

 

행렬과 벡터

 

좌표계는 원점(origin)과 기저(basis) 두 개의 조합으로 이루어진다.

 

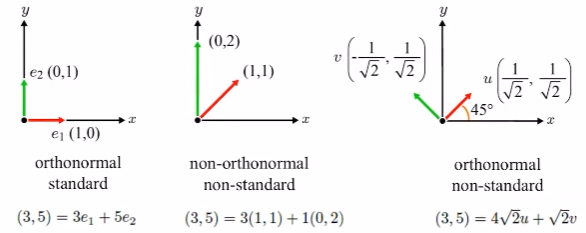
orthonormal basis: 수직이며 normalize 된 기저

non-orthonormal basis: 수직이 아니며 normalize되지 않은 기저

standard basis: x축과 y축에 나란히 있는 기저

non-standard basis: x축과 y축에 나란히 있지 않은 기저

 

 

 

 

Dot Product = Inner Product = 내적

1. 벡터 a, b가 있을 때

 

2. a와 b 사이의 각도 θ가 있을 때, 

 

- a, b가 수직이라면 a · b = 0

- θ가 예각이라면 a · b > 0

- θ가 둔각이라면 a · b < 0

 

orthonormal basis라면 서로의 내적은 0이고, 자기 자신과의 내적은 1임

 

 

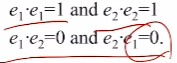
Cross Product = 외적

- 3차원 벡터 사이에서 수행 가능

- a x b 오른손 법칙으로 정의됨

 

1. 벡터 a, b가 있을 때

 

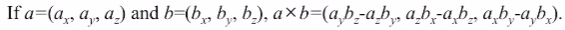
2. a, b 사이의 각도 θ가 있을 때

 

- a = b라면, a x b = (0, 0, 0) 즉, 0임

- a x b = -(b x a), 길이는 같지만 방향이 반대임

 

 

t가 [- ∞ , ∞ ]일 경우 p(t)는 무한한 선이며

t가 [0, ∞]일 경우 p(t)는 ray

t가 [0, 1]일 경우 선분